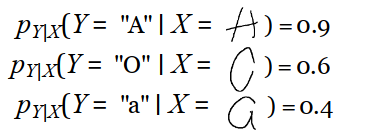Course Info

• 40% 4xAssignments
• 20% 4xQuiz
• 40% Final Project in Wk.13~16

学习

学习的过程

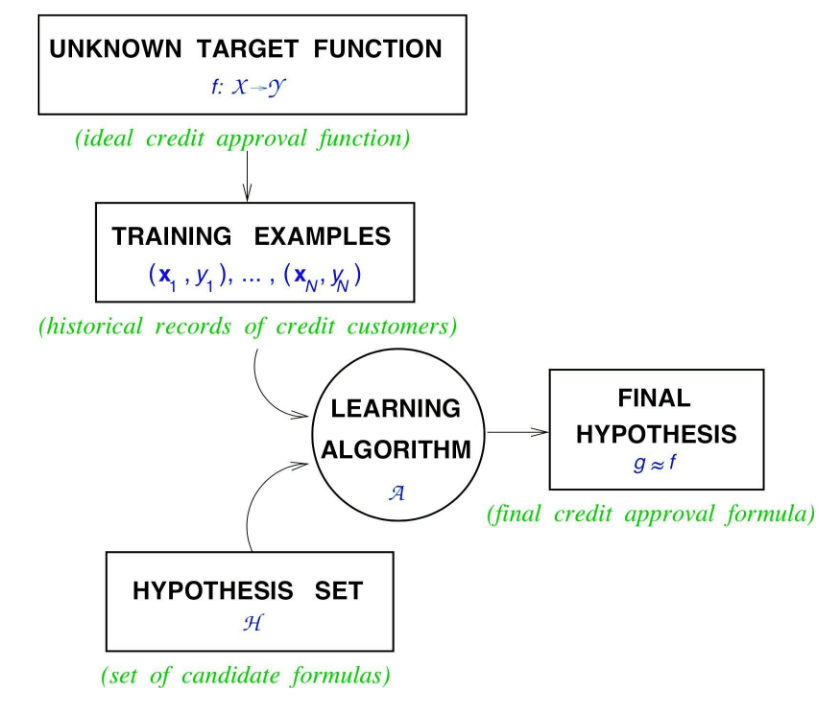
1. 未知目标函数 ($f:\mathcal{X}\to \mathcal{Y}$)：这是理想的、但未知的映射函数，它能够将所有可能的输入正确地映射到输出。在实际问题中，这个函数是不可见的，机器学习的目标就是去近似它。 在图中，它被描述为“理想的信用审批函数”。
2. 训练样本 (($x_1,y_1),\dots ,(x_N,y_N)$)：这些是历史数据记录，包含输入-输出对。学习算法利用这些带有标签的例子来识别模式并进行学习。 在图中，这些是“信用客户的历史记录”。
3. 学习算法 ($\mathcal{A}$)：如前所述，学习算法接收训练样本和假设集。 它的任务是根据训练数据，从假设集中选择一个函数。
4. 假设集 ($\mathcal{H}$)：学习算法从这个“候选公式集”中进行选择。
5. 最终假设 ($g\approx f$)：学习算法的输出是最终的假设，它是一个函数，旨在近似未知目标函数 ($f$)。 在图中，这被称为“最终的信用审批公式”，表示它是一个近似于理想信用审批函数的模型。

学习问题的组件：

• 假设集 ($\mathcal{H}$)：这是一组可能的假设（也称为候选函数或模型），学习算法将从中选择一个。每个假设 ($h$) 都是一个特定的函数，旨在将输入映射到输出。学习算法的目标是从这个假设集中找到一个最能近似目标函数的假设。
• 学习算法 ($\mathcal{A}$)：这是一组规则或过程，机器学习系统使用它来执行任务，通常是为了发现新的数据洞察和模式，或根据给定的输入变量集预测输出值。 学习算法利用训练数据来选择假设集中最能近似未知目标函数的假设。

这两个组件共同被称为学习模型。

感知机

数据和分布

Data & Label

• 在学习中，我们寻求一个从初始数据 $\mathcal{X}$（抽象输入对象的域）到某个标签集 $\mathcal{Y}$（我们想要预测的任何事物）的映射。
• Hypothesis: $h:\mathcal{X}\to \mathcal{Y}$
  • 一个假设是学习算法对输入和输出之间关系的假设
  • 示例：在字符识别中，$\mathcal{X}$ 包含可能的字母图像，$\mathcal{Y}$ 包含拉丁字母表的二十六个字母
  • 为简化起见，我们将使用二元标签 $\{+1,-1\}$。例如，某物是否是字母“G”(+1) 或不是字母“G”(-1)，或者给定图像是否包含人脸 (+1) 或不包含人脸 (-1)。

• 数据 ($\mathcal{X}$)：模型的输入。
• 标签 ($\mathcal{Y}$)：模型的目标输出。
• 假设 ($h$)：一种函数，它尝试从输入数据映射到输出标签

联合分布

• 联合分布 $p_{X,Y}(x,y)$ (是包含两个或多个随机变量的概率分布
• 通过输入的对象及其对应标签，未来数据来自某些未知来源的联合分布 $p_{X,Y}$，我们将其写为联合分布 $p_{X,Y}$，其中 $X\in \mathcal{X},Y\in \mathcal{Y}$
  • Eg. 字符识别源分布会给（“包含圆形形状的图像”，“O”）分配比（“包含圆形形状的图像”，“T”）更高的概率
• 联合分布可以分解为条件概率 (conditional probability)：$p_{Y|X}(y|x)$（在给定输入 $x$ 的情况下，输出 $y$ 的概率）和边际概率 (marginal probability) $p_X(x)$（输入 $x$ 自身的概率）
  • $p_{X,Y}(x,y)=p_{Y|X}(y|x)\cdot p_X(x)$
  • 

概念

• 训练集是一组数据，用于发现潜在的预测关系。
• 测试集是一组用于评估预测关系强度和实用性的数据集。
• 随机分割是划分训练集和测试集的一种常见方法，但并非在所有情况下都适用（例如，时间序列数据、类别不平衡数据可能需要更复杂的分割策略）
• 假设 / Hypothesis：一个假设（预测器 Predictor）$h$ 是从 $\mathcal{X}$ 到 $\mathcal{Y}$ 的函数，$h:\mathcal{X}\to \mathcal{Y}$ (在机器学习中，假设是学习算法对输入和输出之间关系的假设)
• 损失函数 / Loss Function $\text{loss}(h(x),y)$：如何评估 $h$ 在给定（输入、标签）对 $(x,y)$ 上的性能
  • 示例：如果预测的标签 $h(x)$ 与提供的标签 $y$ 不匹配，则损失为 0；如果预测 $h(x)$ 与提供的标签 $y$ 匹配，则损失为 1。
  • 表示这种性能度量的损失函数称为 0-1 损失，其定义如下： $\text{loss}(h(x),y)=\{\begin{array}{ll}1& \text{if }h(x)\ne y\\ 0& \text{if }h(x)=y\end{array}$
• 假设类 / Hypothesis Class，是所有可能假设函数的集合，学习算法将从中选择一个最佳假设，将 $\mathcal{H}$ 定义为预测器集合，写为 $\mathcal{H}=\{h:\mathcal{X}\to \mathcal{Y}\}$
  • 示例：考虑二元标签，即标签集为 $\mathcal{Y}=\{+1,-1\}$。此外，我们可能考虑 $\mathcal{X}={\mathbb{R}}^2$
  • 假设类的一些具体示例：
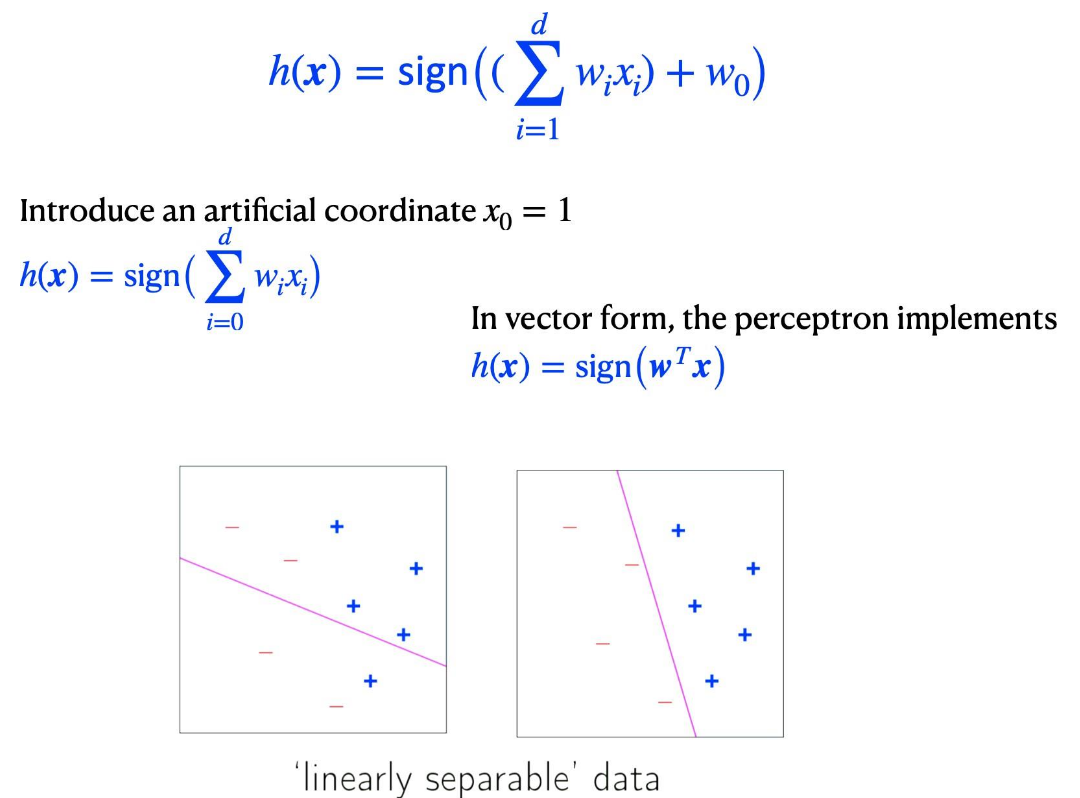
    • 感知机/线性： $\mathcal{H}=\{\text{sign}({\mathbf{w}}^T\mathbf{x}+b)\mid \mathbf{w}\in {\mathbb{R}}^2,b\in \mathbb{R}\}$
    • 半径分类：$\mathcal{H}=\left\{{\sum }_{i=1}^2{x}_i^2\le \theta \mid \theta \in {\mathbb{R}}^{+}\right\}$

• 期望风险 / Expected Risk $R[h]$：在机器学习中，损失函数衡量模型一次预测的误差，而风险函数（期望风险）衡量模型平均预测的误差
  • $R[h]=E_{(X,Y)\sim p_{X,Y}}[\text{loss}(h(x),y)]=\sum _{X,Y}p(x,y)\cdot \text{loss}(h(x),y)$ (对损失函数求期望)
  • AKA. expected loss, generalization error, or source-distribution risk
  • 如果预测器 $h$ 在特定源联合分布上的风险 $R[h]$ 较低，那么它在该分布上就是“良好的”
• 期望风险 $R[h]$ 是预测器 $h$ 对从源联合分布中随机抽取的任何对 $(x,y)$ 的标签预测错误的概率（只适用 0-1 损失）
  • 我们将假设源联合分布是固定的